¿Convolución? ¡Pero si es muy fácil! (Parte 1/3)

Bueno, les comento que para el título del post, saqué la idea de un libro muy viejo que tenía mi abuelo, el cual se titulaba: "¿La Radio? ¡Pero si es muy fácil!", y como me pareció muy simpático para un libro, me quedó grabado muchos años.. ahora lo adapté para usarlo en mi blog :)
Pasando al tema que me toca. La convolución es un tema al que cuesta agarrarle la mano en un principio, tanto en el concepto como el cálculo de la misma. Mientras aprendía este tema, se me ocurrió una forma muy simple de calcular convoluciones a mano, y por eso me decidí a realizar el post. Advierto que no soy un experto en el tema, pero comprendo muy bien el concepto, y voy a tratar de explicarlo de la forma más sencilla posible; además del método de resolución que mencioné y un programa en algún lenguaje que la resuelva, como para terminar esto bien bonito. En la imagen que no se ve, pueden hacer click para agrandarla.
¿Qué es la convolución?
Para comenzar, la convolución se trata de una operación matemática que combina dos señales para producir una tecer señal. En el campo de las señales digitales es muy importante, ya que permite obtener la señal de salida de un sistema a partir de la señal de entrada y la respuesta al impulso. Es decir, podemos predecir la salida, conociendo la entrada y la respuesta al impulso.

Conceptos previos.

Bien, primero que nada, es necesario tener algunas cosas claras antes de explicar la convolución. Comencemos por describir qué es el impulso unitario o función delta (es lo mismo). No es nada más que una simple función matemática que vale 1 en n = 0 y vale 0 en cualquier otro punto. Es decir:

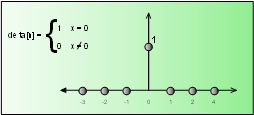
Podemos desplazar y escalar esta función delta, ¿cierto? Por ejemplo, si tenemos una señal s[n] que vale -3 en n = 5 y vale cero en cualquier otro punto, entonces expresarla como una función delta desplazada 5 muestras hacia la derecha, y escalada por un factor de -3. Es decir que s[n] = -3*delta[n-5]. Es decir, lo que tenemos es un impulso (es decir, es una señal que es el impulso unitario pero desplazado y escalado).

Una vez que comprendemos el efecto de desplazar y escalar la función delta, podemos descomponer cualquier señal en una sumatoria de impulsos (funciones delta desplazadas y escaladas). A la descoposición de una señal en una otras señales se le llama análisis de la señal. La idea de esto, es que si tomamos cada impulso y los sumamos, volveremos a obtener la señal original. A la composición de una señal a partir de la sumatoria de otras señales (en nuestro caso impulsos) se le llama síntesis.
Veamos un ejemplo simple de descomposición de una señal en una sumatoria de impulsos
Ahora, imaginemos que tenemos un sistema lineal cualquiera. Si en la entrada de dicho sistema ponemos una señal cuañquiera, el sistema, como es de esperarse, nos devovlerá una señal salida, la cual dependerá exclusivamente de qué haga el sistema internamente. O sea que distintos sistemas nos pueden dar distintas respuestas ante la misma entrada. En el caso particular de que la entrada sea el impulso unitario la salida del sistema se llamará respuesta al impulso o respuesta impulsiva y se denota como h[n].

Lo interesante de esto, es que si la entrada al sistema es un impulso unitario desplazado y escalado, entonces la salida será la respuesta al impulso, pero igualmente desplazada y escalada que que la entrada. Si además, recordamos que cualquier señal puede expesarse como una sumatoria de impulsos, podemos conocer la respuesta del sistema a cada uno de esos impulsos. Y si además, sumamos todas estas respuestas a cada impulso, entonces obtendremos la respuesta del sistema a la señal original.

Ahora si, ¿qué es la convolución?

¿Cuál es el beneficio de todo esto? Que podemos predecir la salida de cualquier sistema linear con solo conocer su respuesta al impulso unitario, es decir, el h[n].y no hay necesidad de introducir realmente una señal de entrada al sistema; sino que descomponemos esa señal en impulsos, evaluamos la respuesta del sistema para cada impulso (escalamos y desplazamos h[n] según cada impulso) y luego sumamos esas respuestas. ¡Todo este proceso, no es más que la convolución de h[n] y la señal de entrada! La convolucion se representa con una estrella. Es decir:

Matemáticamente, se escribe como:

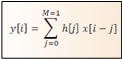
donde M es la cantidad de muestras que tiene la respuesta al impulso h[n] y van desde 0 hasta M-1. La señal x[n] tiene N muestras (0 a N-1). La convolución de ambas señales, y[n], tendrá N+M-1 muestras (de 0 a N+M-2).

Bueno, espero que haya sido claro, sino pregunten o sugieran, y nunca está demás complementar con otras lecturas. Personalmente, recomiendo leer el capítulo 6 de un libro disponible en formato digital llamado "The Scientist and Engineer's Guide to Digital Signal Processing" escrito por Steven W. Smith, Ph.D. Enlace al libro. Está en inglés, ¡pero es excelente!

La proxima entrega describo el método de cálculo manual de la convolución. ¡Nos vemos!
Parte 2